Exercise 2: Recursive time

This exercise about recursive time is still about running time. However, we will try to compare the running time we functions that are recursive and non-recursive in nature. With the code output below, we can see that the recursive function running time takes more time than the non-recursive one. As the m increases, so too the time increases. Let’s take a look at why.

Code Output:

Above is the output of our exercise in this format:

<m> <mth power of 2> <recursive time> <non-recursive time>

This output means that per row, we get the mth power of 2, the value of the mth power of 2, its running time with the recursive function, then the non-recursive function. For example, in the first row, we have 5, so we get 2^5 which is 32, the time it took to calculate that with a recursive function, then the time it took with a non-recursive function.

The recursive function calls itself m number of times until we get the mth power of 2. Imagine how many times it calls itself especially when we started calling out the 20th power of 2. The function would call itself 20 times! How much more if we go further! Comparing this with the non-recursive function, we can see it consumes less time because we only call the function once, and then poof! We got our answer.

T(n) Calculations & Big-Oh

Let’s start with the recursive function:

def powerof2_recursion(n):
  if n == 0:
    return 1
  else:
    return 2 * powerof2_recursion(n-1)

We get T(n) by going through each line of the function:

Let’s assume that n > 0.

1. We compare if n == 0
2. After the else statement, we subtract n – 1
3. We then call the function again powerof2_recursion(n – 1)
4. We multiply that function with 2
5. Then we return all of that
6. Lastly, we include its running time, which is T(n – 1) from powerof2_non_recursion(n – 1)

We have a total of 6 passes when n > 0. But what if n = 0?

1. We compare n == 0
2. Since it’s 0, it then returns 1

A total of 2 Passes.

We have:

Since T(n) of our recursive function is T(n – 1), we’ll do n = n – 1.

We then plug T(n-1) to T(n).

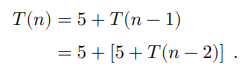
We then see a pattern of the term 5, and we generalize this equation by adding k to how many times 5 is repeated.

When k = n,

Our big-Oh of T(n) = 5n + 2 is O(n), since the largest degree of n we can find is just n. This is the complexity of the recursive algorithm which is n or linear.

Now, with the non-recursive function:

def powerof2_non_recursion(n):
    return 2 ** n

Just seeing the function above, we could say that it is very simple. It just uses 2 lines, the definition of the function, and its return. Let’s go through each line:

1. We get the nth power of 2 by calculating 2 exponent n (2**n)
2. We return the function.

As we can see here, we directly say that it’s’ a constant time. We only have:

Our big-Oh here is O(2) – constant time. It’s that simple.

Conclusion

Comparing both functions, the recursive function takes longer time than the non-recursive one. This is because it iterates again and again till we get our answer. However, for the non-recursive function, we simply pass through it once and we then get our answer. It takes less time than the recursive function, especially when we go with larger numbers. With this, it’s better to use a non-recursive function for this matter.

The code used is below:

import time

# function for power of 2 Using RECURSIVE implementation
def powerof2_recursion(n):
  if n == 0:
    return 1
  else:
    return 2 * powerof2_recursion(n-1)


# function for power of 2 using NON-RECURSIVE implementation
def powerof2_non_recursion(n):
    return 2 ** n


# opening file
with open('input.dat', 'r') as input:
  
  input.readline()
  input_dat = [int(i.strip()) for i in input]


# creating lists for the mth power, recursive time & non-recursive time
mth_power = [2**i for i in input_dat]
recursive_power_time = []
non_recursive_power_time = []


#print(mth_power)


# recording time using recursive implementation
start_time = time.time()
for i in input_dat:

  for j in range(1000000):
    powerof2_recursion(i)
  end_time = time.time()
  recursive_power_time.append(round((end_time - start_time)*1000, 2))


# recording time using non-recursive implementation
start_time = time.time()
for i in input_dat:

  for j in range(1000000):
    powerof2_non_recursion(i)
  end_time = time.time()
  non_recursive_power_time.append(round((end_time - start_time)*1000, 2))


# printing the output
for i in range(len(input_dat)):
  print("{} {} {}ms {}ms".format(input_dat[i], mth_power[i],recursive_power_time[i],non_recursive_power_time[i]))