Exercise 1 – Plotting the Running Time

This exercise focuses on the running time of a code. Here, I had two sorting algorithms – a selection sort function I made (user-defined function), and the built in sorted() function in Python. I expect that the built-in function is faster, because it is *built in*, as compared to the function I made that consumes a little more time, because it has a bunch of lines and it’s not that fully optimized.

Code Output:

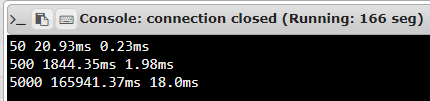
Above is the output of our exercise in this format:

<number of items > <selection sort time> <python sort time>

This means that in the per row, we get the n number of items in the list/array, the selection sort time, then the python sort time. For example, in the first row, we get a list with 50 elements in it, next to it the running time when we sort it using our user-defined selection sort and after it, the python sorted function time.

We can see here that our python sort time (the built in sorted function), is way lesser than the selection sort time (the function I just made). I compared both of the functions through its Big Oh ( O(n) ) notation. The built in sorted() function is in log-linear time complexity ( O(nlogn) ) while my user-defined function is in the quadratic complexity ( O(n^2) ). Note that having more complexity is worse. So in this example, the built in sorted() function is more efficient.

The difficulties I encountered is mainly about getting back to coding. It’s been a while since I code, and also, I’ve got other subjects that had deadlier deadlines. I’ve been practicing Python over the “break” but never really gotten deeper. So, in this exercise, I searched a lot in the net. About opening a file, we never had that in class nor did I learn the syntax for it in previous discussions during my first year, so I had to research about it. Fortunately, when I got lost, I’ve got my friends who helped me.

With the question about, “Will there ever be a case where I’ll choose the quadratic time algorithm over the log-linear one in terms of running time? “, it depends on the situation. However, I’ll use mostly the algorithm with less complexity so that it’s more efficient. I can save more time and resources used by the computer. That’s all I can say for now, knowing that I still have limited exposure in programming in a higher level, especially in data structures. I’ll continue to learn more about this topic and grow from this.

The code used is below:

import time

# Selection Sort Function
def selection_sort(lst):

  for i in range(len(lst)-1): 
    min = i
    for j in range(i, len(lst)):
      if lst[j] < lst[min]:
        min = j
    
    temp = lst[i]
    lst[i] = lst[min]
    lst[min] = temp

  return lst


input_dat = [] # List of for the input.dat

# Opening the file
with open("input.dat", 'r') as input:

  input_dat = [ # List comprehension to fill up the list
    [int(val) for val in line.split()] 
    for line in input.readlines() 
    if len(line.split()) > 1
    ]
      
        
#print(input_dat)


selection_sort_time = []
python_sort_time = []


# Recording the time for the Selection Sort Function
start_time = time.time()
for i in input_dat:

  for j in range(100):
    selection_sort(i)
  
  end_time = time.time()
  selection_sort_time.append(round((end_time - start_time)*1000,2))


# Recording the time for the built-in Python Sort Function
start_time = time.time()
for i in input_dat:

  for j in range(100):
    sorted(i)
  
  end_time = time.time()
  python_sort_time.append(round((end_time - start_time)*1000,2))


# Printing out the number of contents of the list, its selection sort time, and python sort time. 
# These 3 are all in their respective list.
for i in range(len(input_dat)):
  print("{len} {sel}ms {py}ms".format(len=len(input_dat[i]), sel=selection_sort_time[i], py=python_sort_time[i]))